2024-25
News
The course will be taught in English. Of course the students may ask questions in Portuguese if they prefer, but (if the discussion is public) the teacher's answers will be in English. Answers to practical assigments and to the final written exam may be given in either languange.
We will not use Moodle.
Avaliação
A avaliação terá duas componentes : trabalhos práticos e exame final.
Os trabalhos são individuais e diferentes de aluno para aluno. Cada aluno deverá escolher (duma lista) trabalhos cujo valor somado deve estar entre 2 e 10. Os trabalhos devem ser entregues até ao dia do exame de primeira data.
Os trabalhos podem ser resolvidos em grupo; nesse caso, a cotação será dividida entre os membros do grupo.
O exame final vai focar sobre a parte teórica, valerá entre 10 e 18 valores, em função da escolha dos trabalhos.
Exemplo : o aluno A escolhe trabalhos no valor total 5, mas o professor considera o resultado insatisfatório e o aluno fica com a nota 3. O aluno B escolhe trabalhos no valor total 10, o professor avalia esses trabalhos em 9. O aluno A faz o exame para 15 valores, o aluno B faz o mesmo exame para 10 valores.
No exame de segunda data, o aluno poderá escolher entre manter a nota dos trabalhos práticos ou fazer exame para 20 valores.
No exame é permitido o uso de calculadoras gráficas. Cada aluno pode ter uma folha A4 com apontamentos, escrita de ambos os lados.
Perguntas modelo para exame :
Practical assignements
Computational geometry
PA-1-1 (1v) Compute the perimeter of a polygon. Chosen by Beatriz Correia
PA-1-2 (4v) Compute the area of a convex polygon. Bonus 3v for non-convex polygons. Chosen by Beatriz Correia
PA-1-3 (4v) Given three points A, B and C and a natural number n, divide the triangle ABC in smaller triangles. Bonus 4v for curved sides. Bonus 2v for graphical output. Chosen by Mariana Miranda
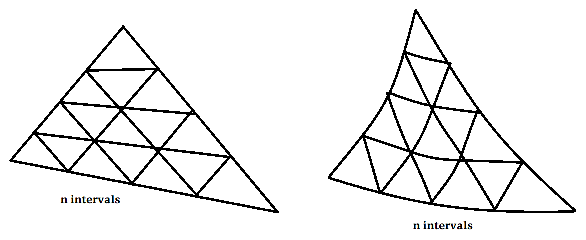
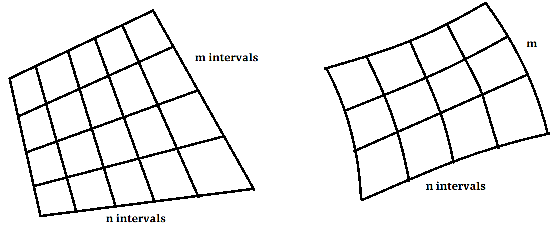
PA-1-4 (4v) Given four points A, B, C and D and two natural numbers m and n, divide the quadrilateral ABCD in smaller quadrilaterals. Bonus 4v for curved sides. Bonus 2v for graphical output. Chosen by Eva Paiva
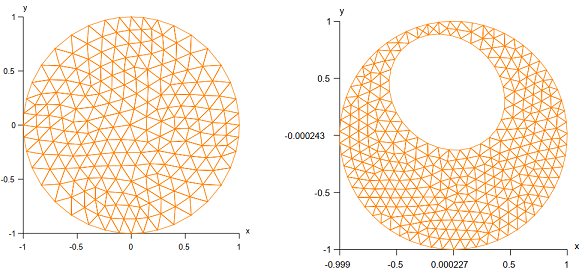
PA-1-5 (7v) Given a plane region and a desired segment size s, divide the region in triangles with sides length approximately equal to s. Bonus 5v for regions with holes. Bonus 2v for graphical output. Chosen by Ana Caseiro
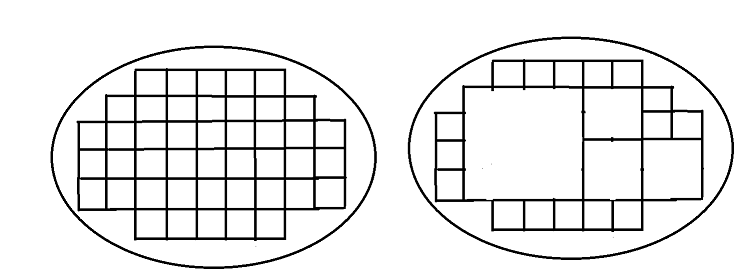
PA-1-6 (6v) Given a plane region and a desired segment size s, fill most of the region with squares of size s. Bonus 5v for joining inner squares into larger ones. Bonus 2v for graphical output. Chosen by Mariana Martins
PA-1-7 (2v) We are given a cloud of points and a subset of "privileged" points, drawn below in blue. We can imagine the blue points as a river. We want to compute, for each black point, the distance to the river, that is, the distance to the nearest blue point. Bonus 2v for graphical output, using color as an indicator of the distance. Bonus 4v for efficiency, using (as input) a list of nearest neighbours of each point. Chosen by Carolina Ferreira
Linear algebra
Solving systems of linear equations, direct methods
PA-2-1 (4v) Compute the determinant of a square matrix by taking into account all possible permutations of indices. Chosen by Antonio Alampi
PA-2-2 (4v) Compute the determinant of a square matrix by developing along a row or a column. Chosen by Mariana Miranda
PA-2-3 (4v) Implement the gaussian elimination algorithm. Chosen by Hugo Nunes
PA-2-4 (4v) Add to PA-2-3 pivot searching (switching rows). Chosen by Ana Correia
PA-2-5 (4v) Add to PA-2-3 total pivot searching (switching rows and columns). Chosen by Ana Correia
PA-2-6 (3v) Adapt PA-2-3 to tridiagonal matrices. Bonus 2v for band matrices. Chosen by Tomás Lopes
PA-2-7 (4v) Adapt PA-2-3 for solving simultaneously several systems of equations with the same matrix A (different vectors b). Chosen by Bárbara Clemente
PA-2-8 (4v) Adapt PA-2-4 for solving simultaneously several systems of equations with the same matrix A (different vectors b).
PA-2-9 (4v) Adapt PA-2-5 for solving simultaneously several systems of equations with the same matrix A (different vectors b). Chosen by Gonçalo Carvalhão
Solving systems of linear equations, iterative methods
PA-3-1 (4v) Implement the Gauss-Seidel algorithm for solving a system of linear equations. Chosen by Raquel Bravo
PA-3-2 (4v) Implement the Gauss-Seidel algorithm with row switching. Chosen by Mariana Martins
PA-3-3 (4v) Implement the Gauss-Seidel algorithm with row and column switching. Chosen by Margarida Patrocínio
PA-3-4 (3v) Implement the Gauss-Seidel algorithm with relaxation. Chosen by Gonçalo Carvalhão
PA-3-5 (3v) Adapt PA-3-1 for band matrices. Chosen by José Santana
PA-3-6 (3v) Adapt PA-3-4 for band matrices. Chosen by José Santana
Computing eigenvalues and eigenvectors
PA-4-1 (5v) Implement the power method. Chosen by Beatriz Correia
PA-4-2 (3v) Implement the power method with a translation. Chosen by José Santana
PA-4-3 (3v) Implement the inverse power method, using at each step the technique in PA-2-7.
PA-4-4 (3v) Implement the inverse power method, using at each step the technique in PA-2-8.
PA-4-5 (3v) Implement the inverse power method, using at each step the technique in PA-2-9.
PA-4-6 (3v) Implement the inverse power method, using at each step the technique in PA-3-1.
PA-4-7 (3v) Implement the inverse power method, using at each step the technique in PA-3-4. Chosen by Gonçalo Carvalhão
PA-4-8 (3v) Improve the method in PA-4-3 by adding a translation.
PA-4-9 (3v) Improve the method in PA-4-4 by adding a translation.
PA-4-10 (3v) Improve the method in PA-4-5 by adding a translation.
PA-4-11 (3v) Improve the method in PA-4-6 by adding a translation.
PA-4-12 (3v) Improve the method in PA-4-7 by adding a translation.
Solving non-linear equations in one variable
PA-5-1 (3v) Implement the bisection method. Chosen by Joana Santos
PA-5-2 (3v) Implement the fixed point method. Chosen by Bárbara Clemente
PA-5-3 (3v) Implement the Newton-Raphson method. Chosen by Eva Paiva
PA-5-4 (3v) Implement the secant method.
PA-5-5 (3v) Implement the method of false position. Bonus 2v for improving the method by alternating steps of bisection method and secant method.
Solving systems of non-linear equations
PA-6-1 (4v) Implement the fixed point method for systems of equations.
PA-6-2 (5v) Implement Newton's method for systems of equations. At each step, the system of linear equations should be solved by Gaussian elimination
PA-6-3 (5v) Implement Newton's method for systems of equations. At each step, the system of linear equations should be solved by Gaussian elimination with row switching
PA-6-4 (5v) Implement Newton's method for systems of equations. At each step, the system of linear equations should be solved by Gaussian elimination with row and column switching
PA-6-5 (5v) Implement Newton's method for systems of equations. At each step, the system of linear equations should be solved by Gauss-Seidel algorithm; the solution from the previous step should be used as starting point
PA-6-6 (5v) Implement Newton's method for systems of equations. At each step, the system of linear equations should be solved by Gauss-Seidel algorithm with relaxation (SOR); the solution from the previous step should be used as starting point